COA Tutorial
Basic CO and Design
Computer Instructions
Digital Logic Circuits
Map Simplification
Combinational Circuits
Flip - Flops
Digital Components
Register Transfer
Micro-Operations
Memory Organization
COA_Misc
- Booth's Multiplication Algorithm
- Branch Instruction in Computer Organization
- Data Representation in Computer Organization
- ALU and Data Path in Computer Organization
- External memory in Computer Organization
- Structured Computer Organization
- Types of Register in Computer Organization
- Secondary Storage Devices in Computer Organization
- Types of Operands in Computer Organization
- Serial Communication in Computer organization
- Addressing Sequencing in Computer Organization
- Simplified Instructional Computer (SIC)
- Arithmetic Instructions in AVR microcontroller
- Conventional Computing VS Quantum Computing
- Instruction set used in Simplified Instructional Computer
- Branch Instruction in AVR microcontroller
- Conditional Branch instruction in AVR Microcontroller
- Data transfer instruction in AVR microcontroller
- Difference between Memory-based and Register-based addressing modes
- Difference between 1's complement Representation and 2's complement Representation
- CALL Instructions and Stack in AVR Microcontroller
- Difference between Call and Jump Instructions
- Overflow in Arithmetic Addition in Binary number System
- Horizontal Micro-programmed Vs. Vertical Micro-programmed Control Unit
- Hardwired Vs. Micro-programmed Control Unit
- Non-Restoring Division Algorithm for Unsigned Integer
- Restoring Division Algorithm for Unsigned Integer
- Debugging a Machine-level Program
- Dependencies and Data Hazard in pipeline in Computer Organization
- Execution, Stages and Throughput in Pipeline
- Types of Pipeline Delay and Stalling
- Timing Diagram of MOV Instruction
- Advantages and Disadvantages of Flash Memory
- Importance/Need of negative feedback in amplifiers
- Anti-Aliasing - Computer Graphics
- Bus Arbitration in Computer Organization
- Convert a number from Base 2 (Binary) to Base 6
- Cache Coherence
- EHCI
- Cache Memory and Virtual Memory
- Electrical Potential and Potential Difference
- RAM and Cache
- SIM and RIM instructions in 8085 processor
- Clusters in Computer Organization
- Data Types and Addressing Modes of 80386/80386DX Microprocessor
Restoring Division Algorithm for Unsigned Integer
Restoring division is usually performed on the fixed point fractional numbers. When we perform division operations on two numbers, the division algorithm will give us two things, i.e., quotient and remainder. This algorithm is based on the assumption that 0 < D < N. With the help of digit set {0, 1}, the quotient digit q will be formed in the restoring division algorithm. The division algorithm is generally of two types, i.e., fast algorithm and slow algorithm. Goldschmidt and Newton-Raphson are the types of fast division algorithm, and STR algorithm, restoring algorithm, non-performing algorithm, and the non-restoring algorithm are the types of slow division algorithm.
In this section, we are going to perform restoring algorithm with the help of an unsigned integer. We are using restoring term because we know that the value of register A will be restored after each iteration. We will also try to solve this problem using the flow chart and apply bit operations.
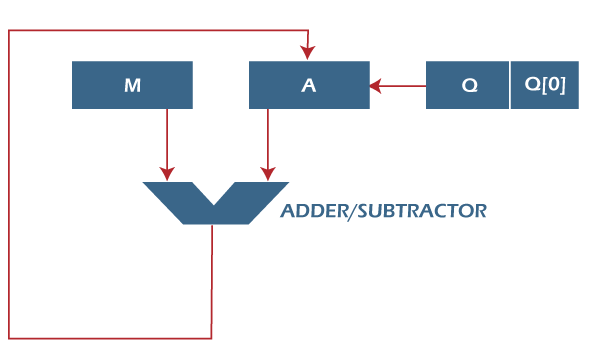
Here, register Q is used to contain the quotient, and register A is used to contain the remainder. Here, the divisor will be loaded into the register M, and n-bit divided will be loaded into the register Q. 0 is the starting value of a register. The values of these types of registers are restored at the time of iteration. That's why it is known as restoring.
Hello Java Program for Beginners
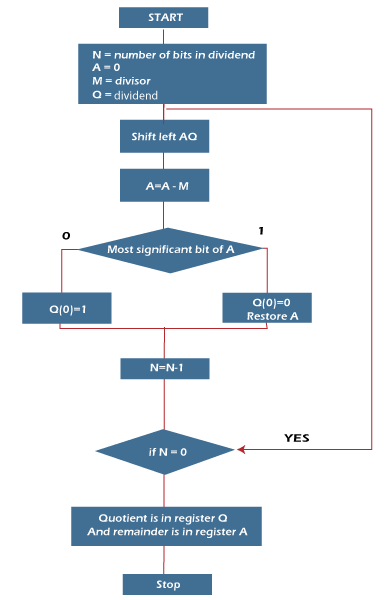
Now we will learn some steps of restoring division algorithm, which is described as follows:
Step 1: In this step, the corresponding value will be initialized to the registers, i.e., register A will contain value 0, register M will contain Divisor, register Q will contain Dividend, and N is used to specify the number of bits in dividend.
Step 2: In this step, register A and register Q will be treated as a single unit, and the value of both the registers will be shifted left.
Step 3: After that, the value of register M will be subtracted from register A. The result of subtraction will be stored in register A.
Step 4: Now, check the most significant bit of register A. If this bit of register A is 0, then the least significant bit of register Q will be set with a value 1. If the most significant bit of A is 1, then the least significant bit of register Q will be set to with value 0, and restore the value of A that means it will restore the value of register A before subtraction with M.
Step 5: After that, the value of N will be decremented. Here n is used as a counter.
Step 6: Now, if the value of N is 0, we will break the loop. Otherwise, we have to again go to step 2.
Step 7: This is the last step. In this step, the quotient is contained in the register Q, and the remainder is contained in register A.
For example:
In this example, we will perform a Division restoring algorithm.
- Dividend = 11
- Divisor = 3
| N | M | A | Q | Operation |
| 4 | 00011 | 00000 | 1011 | Initialize |
| 00011 | 00001 | 011_ | Shift left AQ | |
| 00011 | 11110 | 011_ | A = A - M | |
| 00011 | 00001 | 0110 | Q[0] = 0 And restore A | |
| 3 | 00011 | 00010 | 110_ | Shift left AQ |
| 00011 | 11111 | 110_ | A = A - M | |
| 00011 | 00010 | 1100 | Q[0] = 0 | |
| 2 | 00011 | 00101 | 100_ | Shift left AQ |
| 00011 | 00010 | 100_ | A = A - M | |
| 00011 | 00010 | 1001 | Q[0] = 1 | |
| 1 | 00011 | 00101 | 001_ | Shift left AQ |
| 00011 | 00010 | 001_ | A = A - M | |
| 00011 | 00010 | 0011 | Q[0] = 1 |
So we should not forget to restore the value of the most significant bit of A, which is 1. So, register A contains the remainder 2, and register Q contains the quotient 3.