The Map method involves a simple, straightforward procedure for simplifying Boolean expressions.

Map simplification may be regarded as a pictorial arrangement of the truth table which allows an easy interpretation for choosing the minimum number of terms needed to express the function algebraically. The map method is also known as Karnaugh map or K-map.

Each combination of the variables in a truth table is called a mid-term.

Note: When expressed in a truth table a function of n variables will have 2^n min-terms, equivalent to the 2^n binary numbers obtained from n bits.

There are four min-terms in a two variable map. Therefore, the map consists of four squares, one for each min-term. The 0's and 1's marked for each row, and each column designates the values of variable x and y, respectively.

Two-variable map:

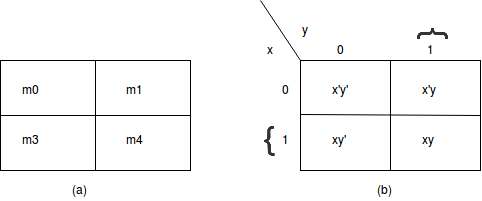
Representation of functions in the two-variable map:

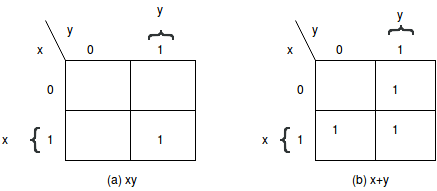
Three variable map

There are eight min-terms in a three-variable map. Therefore, the map consists of eight squares.

Three variable map:

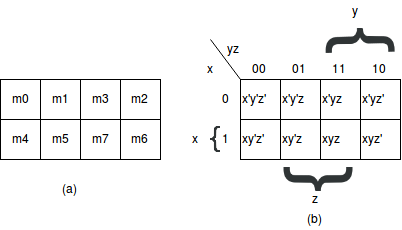
• The map was drawn in part (b) in the above image is marked with numbers in each row and each column to show the relationship between the squares and the three variables.
• Any two adjacent squares in the map differ by only one variable, which is primed in one square and unprimed in the other. For example, m5 and m7 lie in the two adjacent squares. Variable y is primed in m5 and unprimed in m7, whereas the other two variables are the same in both the squares.
• From the postulates of Boolean algebra, it follows that the sum of two min-terms in adjacent squares can be simplified to a single AND term consisting of only two literals. For example, consider the sum of two adjacent squares say m5 and m7:
  m5+m7 = xy'z+xyz= xz(y'+y)= xz.