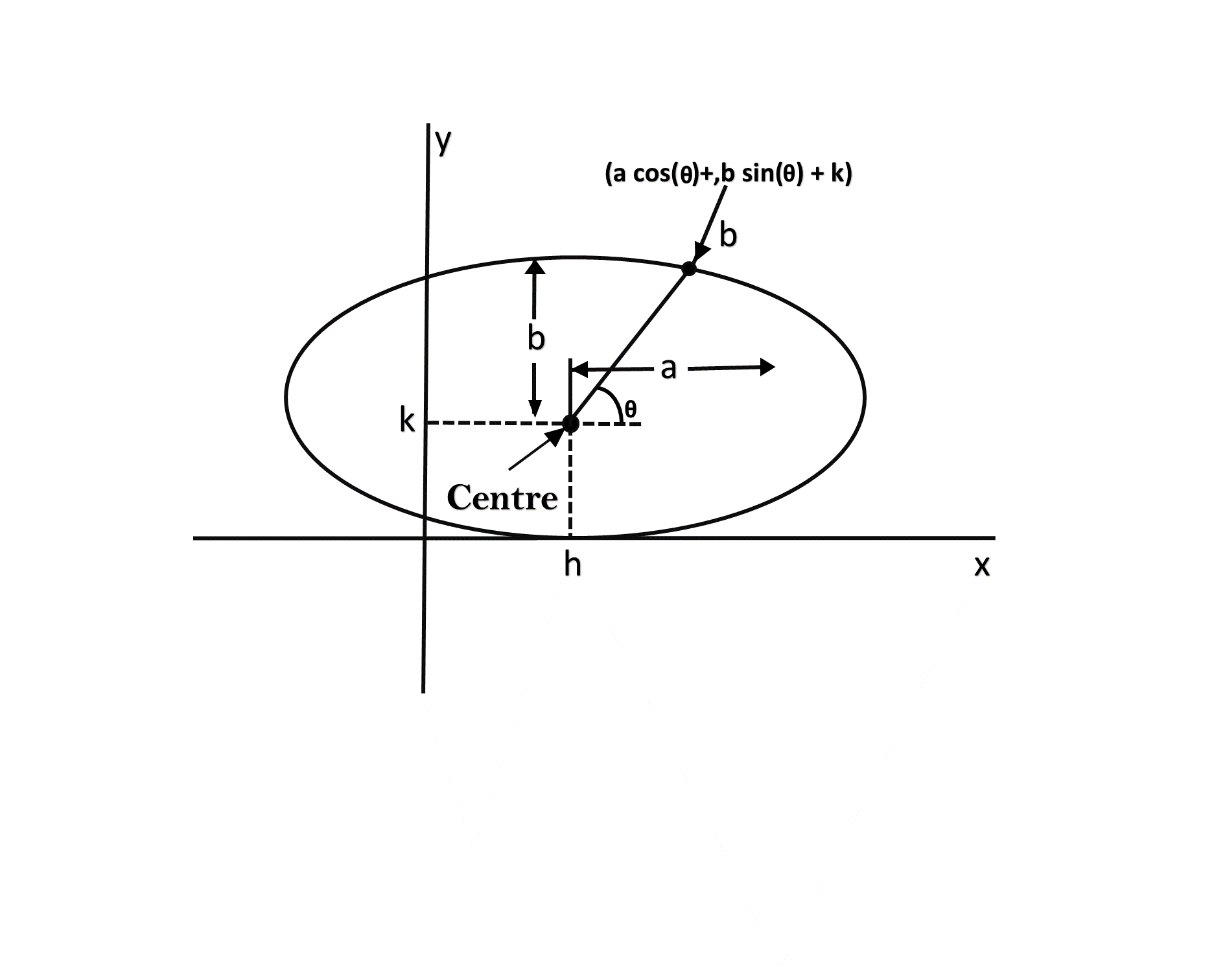
The following equation defines an ellipse trigonometrically as shown in fig:

x = a * cos (θ) +h and
y = b * sin (θ)+k
where (x, y) = the current coordinates
a = length of major axis
b = length of minor axis
θ= current angle
(h, k) = ellipse center

In this method, the value of θ is varied from 0 to 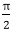 radians. The remaining points are found by symmetry.

Exception Handling in Java - Javatpoint

Drawback:

1. This is an inefficient method.
2. It is not an interactive method for generating ellipse.
3. The table is required to see the trigonometric value.
4. Memory is required to store the value of θ.

Algorithm:

Step1: Start Algorithm

Step2: Declare variable x₁,y₁,aa₁,bb₁,aa₂,bb₂,fx,fy,p1,a1,b1

Step3: Initialize x₁=0 and y₁=b/* values of starting point of circle */

Step4: Calculate aa₁=a₁*a₁
          Calculate bb₁=b₁* b₁
          Calculate aa₂=aa₁*2
          Calculate bb₂=bb₁*2

Step5: Initialize fx = 0

Step6: Initialize fy = aa_2* b₁

Step7: Calculate the value of p₁and round if it is integer
          p₁=bb₁-aa₁* b₁+0.25* aa₁/

Step8:

While (fx < fy)
	{
		Set pixel (x1,y1)
                      Increment x i.e., x = x + 1
                      Calculate fx = fx + bb2
                       If (p1 < 0)
                                 Calculate p1 = p1 + fx + bb1/
                       else
		{
			Decrement y i.e., y = y-1
	                      Calculate fy = fy - 992;
				p1=p1 + fx + bb1-fy
                        }
                }

Step9: Setpixel (x₁,y₁)

Step10: Calculate p1=bb₁ (x+.5)(x+.5)+aa(y-1)(y-1)-aa₁*bb₁

Step 11:

While (y1>0)
                {
                          Decrement y i.e., y = y-1
                           fy=fx-aa2/
                         if (p1>=0)
		   p1=p1 - fx +  aa1/
                        else
                 {
                        Increment x i.e., x = x + 1
                        fx= fx+bb_2
                        p1=p1+fx-fy-aa1
                  }
        }
       Set pixel (x1,y1)

Step12: Stop Algorithm

Program to draw a circle using Trigonometric method:

1. #include <graphics.h>  
2. #include <stdlib.h>  
3. #include <math.h>  
4. #include <stdio.h>  
5. #include <conio.h>  
6. #include <iostream.h>  
7. # define pi 3.14  
8.   
9. class bresen  
10. {  
11.     float a, b, h, k, thetaend,step,x,y;  
12.     int i;  
13.     public:  
14.     void get ();  
15.     void cal ();  
16. };  
17.     void main ()  
18.     {  
19.     bresen b;  
20.     b.get ();  
21.     b.cal ();  
22.     getch ();  
23.    }  
24.     void bresen :: get ()  
25.    {  
26.     cout<<"\n ENTER CENTER OF ELLIPSE";  
27.     cin>>h>>k;  
28.     cout<<"\n ENTER LENGTH OF MAJOR AND MINOR AXIS";  
29.     cin>>a>>b;  
30.     cout<<"\n ENTER STEP SIZE";  
31.     cin>> step;  
32.    }  
33. void bresen ::cal ()  
34. {  
35.     /* request auto detection */  
36.     int gdriver = DETECT,gmode, errorcode;  
37.     int midx, midy, i;  
38.     /* initialize graphics and local variables */  
39.     initgraph (&gdriver, &gmode, " ");  
40.     /* read result of initialization */  
41.     errorcode = graphresult ();  
42.     if (errorcode ! = grOK)    /*an error occurred */  
43.     {  
44.         printf("Graphics error: %s \n", grapherrormsg (errorcode);  
45.         printf ("Press any key to halt:");  
46.         getch ();  
47.         exit (1); /* terminate with an error code */  
48.     }  
49.     theta= 0;  
50.     thetaend=(pi*90)/180;  
51.     whilex (theta<thetaend)  
52.     {  
53.         x = a * cos (theta);  
54.         y = b * sin (theta);  
55.         putpixel (x+h, y+k, RED);  
56.         putpixel (-x+h, y+k, RED);  
57.         putpixel (-x+h, -y+k, RED);  
58.         putpixel (x+h, -y+k, RED);  
59.         theta+=step;  
60.     }  
61.         getch();  
62. }  

Output:

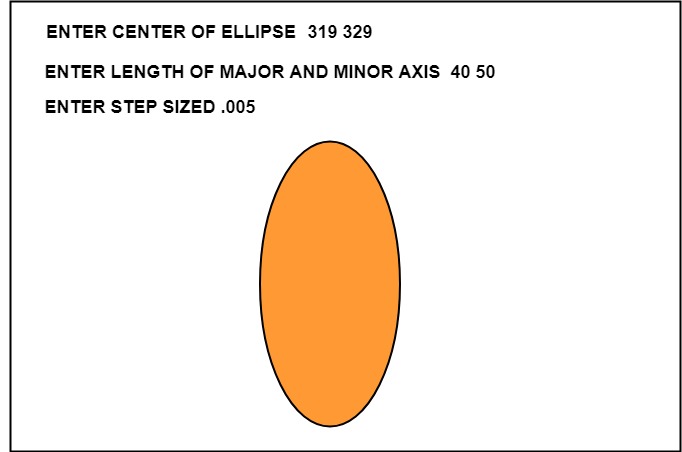
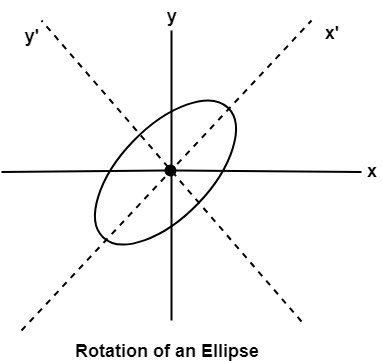
Ellipse Axis Rotation:

Since the ellipse shows four-way symmetry, it can easily be rotated. The new equation is found by trading a and b, the values which describe the major and minor axes. When the polynomial method is used, the equations used to describe the ellipse become

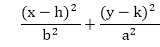
where (h, k) = ellipse center
a = length of the major axis
b = length of the minor axis
In the trigonometric method, the equations are
x = b cos (θ)+h       and       y=a sin(θ)+k

Where (x, y) = current coordinates
a = length of the major axis
b = length of the minor axis
θ = current angle
(h, k) = ellipse center

Assume that you would like to rotate the ellipse through an angle other than 90 degrees. The rotation of the ellipse may be accomplished by rotating the x &y axis α degrees.

          x = a cos (0) - b sin (0+ ∞) + h y= b (sin 0) + a cos (0+∞) + k