Computer Graphics
Graphic Systems
Input-Output Devices
Scan Conversion a line
Scan Conversion Circle
Scan Converting Ellipse
Filled Area Primitives
2D Transformations
2D-Viewing
Clipping Techniques
Pointing & Positioning
3D Computer Graphics
Hidden Surfaces
Projection
Programs
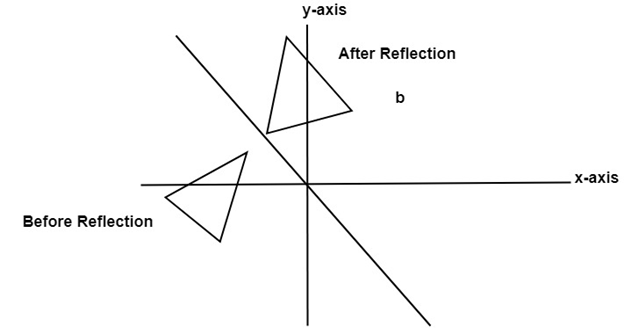
Reflection
is a transformation which produces a mirror image of an object. The mirror image can be either about x-axis or y-axis. The object is rotated by180°.
Types of Reflection:
- Reflection about the x-axis
- Reflection about the y-axis
- Reflection about an axis perpendicular to xy plane and passing through the origin
- Reflection about line y=x
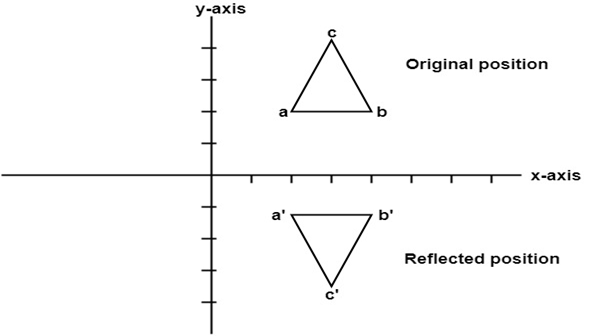
1. Reflection about x-axis: The object can be reflected about x-axis with the help of the following matrix
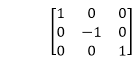
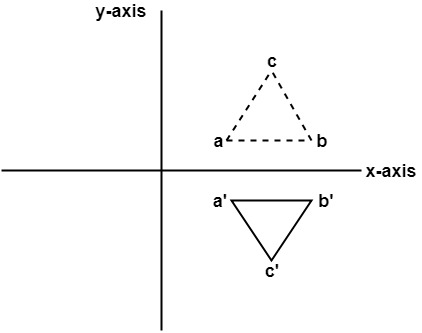
In this transformation value of x will remain same whereas the value of y will become negative. Following figures shows the reflection of the object axis. The object will lie another side of the x-axis.
Polymorphism in Java | Dynamic Method Dispatch
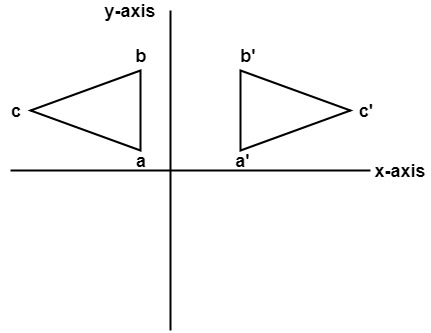
2. Reflection about y-axis: The object can be reflected about y-axis with the help of following transformation matrix
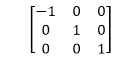
Here the values of x will be reversed, whereas the value of y will remain the same. The object will lie another side of the y-axis.
The following figure shows the reflection about the y-axis
3. Reflection about an axis perpendicular to xy plane and passing through origin:
In the matrix of this transformation is given below
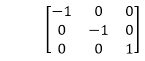
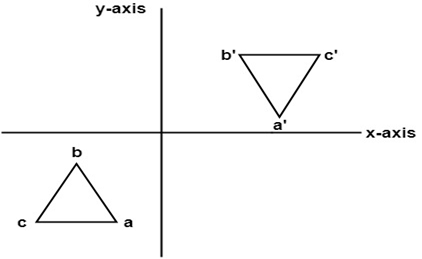
In this value of x and y both will be reversed. This is also called as half revolution about the origin.
4. Reflection about line y=x: The object may be reflected about line y = x with the help of following transformation matrix
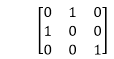
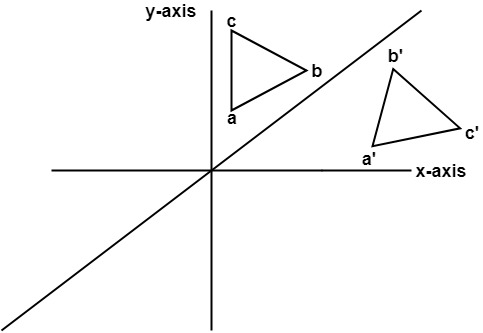
First of all, the object is rotated at 45°. The direction of rotation is clockwise. After it reflection is done concerning x-axis. The last step is the rotation of y=x back to its original position that is counterclockwise at 45°.
Example: A triangle ABC is given. The coordinates of A, B, C are given as
A (3 4)
B (6 4)
C (4 8)
Find reflected position of triangle i.e., to the x-axis.
Solution:

The a point coordinates after reflection
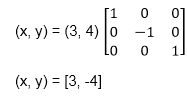
The b point coordinates after reflection
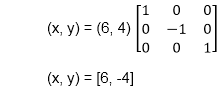
The coordinate of point c after reflection
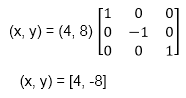
a (3, 4) becomes a1 (3, -4)
b (6, 4) becomes b1 (6, -4)
c (4, 8) becomes c1 (4, -8)
Program to perform Mirror Reflection about a line:
- #include <iostream.h>
- #include <conio.h>
- #include <graphics.h>
- #include <math.h>
- #include <stdlib.h>
- #define pi 3.14
- class arc
- {
- float x[10],y[10],theta,ref[10][10],ang;
- float p[10][10],p1[10][10],x1[10],y1[10],xm,ym;
- int i,k,j,n;
- public:
- void get();
- void cal ();
- void map ();
- void graph ();
- void plot ();
- void plot1();
- };
- void arc::get ()
- {
- cout<<"\n ENTER ANGLE OF LINE INCLINATION AND Y INTERCEPT";
- cin>> ang >> b;
- cout <<"\n ENTER NO OF VERTICES";
- cin >> n;
- cout <<"\n ENTER";
- for (i=0; i<n; i++)
- {
- cout<<"\n x["<<i<<"] and y["<<i<<"]";
- }
- theta =(ang * pi)/ 180;
- ref [0] [0] = cos (2 * theta);
- ref [0] [1] = sin (2 * theta);
- ref [0] [2] = -b *sin (2 * theta);
- ref [1] [0] = sin (2 * theta);
- ref [1] [1] = -cos (2 * theta);
- ref [1] [2] = b * (cos (2 * theta)+1);
- ref [2] [0]=0;
- ref [2] [1]=0;
- ref [2] [2] = 1;
- }
- void arc :: cal ()
- {
- for (i=0; i < n; i++)
- {
- p[0] [i] = x [i];
- p [1] [i] = y [i];
- p [2] [i] = 1;
- }
- for (i=0; i<3;i++)
- {
- for (j=0; j<n; j++)
- {
- p1 [i] [j]=0;
- for (k=0;k<3; k++)
- }
- p1 [i] [j] + = ref [i] [k] * p [k] [j];
- }
- for (i=0; i<n; i++)
- {
- x1 [i]=p1[0] [i];
- y1 [i] = p1 [1] [i];
- }
- }
- void arc :: map ()
- {
- int gd = DETECT,gm;
- initgraph (&gd, &gm, " ");
- int errorcode = graphresult ();
- /* an error occurred */
- if (errorcode ! = grOK)
- {
- printf ("Graphics error: %s \n", grapherrormsg (errorcode));
- printf ("Press any key to halt:");
- getch ();
- exit (1); /* terminate with an error code */
- }
- }
- void arc :: graph ()
- {
- xm=getmaxx ()/2;
- ym=getmaxy ()/2;
- line (xm, 0, xmm 2*ym);
- }
- void arc :: plot 1 ()
- {
- for (i=0; i <n-1; i++)
- {
- circle (x1[i]+xm, (-y1[i]+ym), 2);
- line (x1[i]+xm, (-y1[i]+ym), x1[i+1]+xm, (-y1[i+1]+ym));
- }
- line (x1[n-1)+xm, (-y1[n-1]+ym), x1[0]+xm, (-y1[0]+ym));
- getch();
- }
- void arc :: plot ()
- {
- for (i=0; i <n-1; i++)
- {
- circle (x1[i]+xm, (-y1[i]+ym, 2);
- line (x1[i]+xm, (-y1[i]+ym), x[i+1]+xm, (-y1[i+1]+ym));
- }
- line (x[n-1]+xm, (-y1[n-1]+ym), x[0]+xm, (-y[0]+ym));
- getch();
- }
- void main ()
- {
- class arc a;
- clrscr();
- a.map();
- a.graph();
- a.get();
- a.cal();
- a.plot();
- a.plot1();
- getch();
- }
Output: