Elastic or Rubber Band Techniques
Rubber banding is a popular technique of drawing geometric primitives such as line, polylines, rectangle, circle and ellipse on the computer screen.
It becomes an integral part and de facto standard with the graphical user interface (GUI) for drawing and is almost universally accepted by all windows based applications.
The user specifies the line in the usual way by positioning its two endpoints. As we move from the first endpoint to the second, the program displays a line from the first endpoint to the cursor position, thus he can see the lie of the line before he finishes positioning it.
Difference between JDK, JRE, and JVM
The effect is of an elastic line stretched between the first endpoint and the cursor; hence the name for these techniques.
Consider the different linear structures in fig (a) and fig (d), depending on the position of the cross-hair cursor. The user may move the cursor to generate more possibilities and select the one which suits him for a specific application.
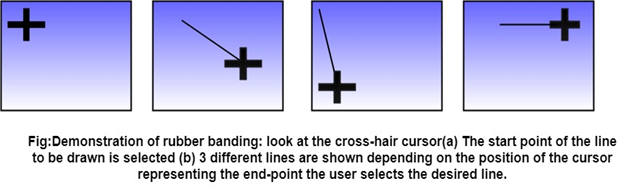
Selection of Terminal Point of the Line:
The user moves the cursor to the appropriate position and selects.
Then, as the cursor is moved, the line changes taking the latest positions of the cursors as the end-point.
As long as the button is held down, the state of the rubber band is active.
The process is explained with the state transition diagram of rubber banding in fig:
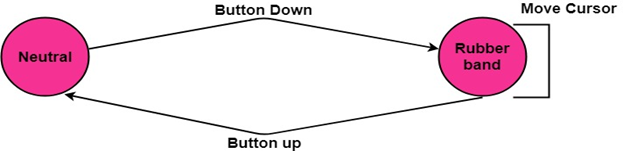
When the user is happy with the final position, the pressed button is released, and the line is drawn between the start and the last position of the cursor.
Example: This is widely followed in MS-Window based Applications like in the case of a paintbrush drawing package.
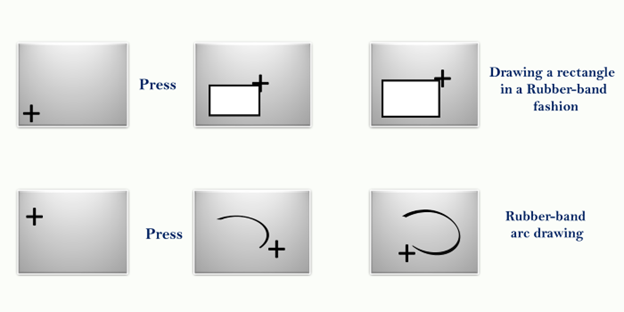
Other geometric entities can be drawn in a rubber-band fashion:
- Horizontally or vertically constructed lines
- Rectangles
- Arcs of circles
This technique is very helpful in drawing relatively complex entities such as rectangles and arcs.
Advantage:
- It is used for drawing all geometric entities such as line, polygon, circle, rectangle, ellipse, and other curves.
- It is easy to understand and implement.
Disadvantage:
- It requires computational resources like software and CPU speed.
- Expensive
