Computer Graphics
Graphic Systems
Input-Output Devices
Scan Conversion a line
Scan Conversion Circle
Scan Converting Ellipse
Filled Area Primitives
2D Transformations
2D-Viewing
Clipping Techniques
Pointing & Positioning
3D Computer Graphics
Hidden Surfaces
Projection
Programs
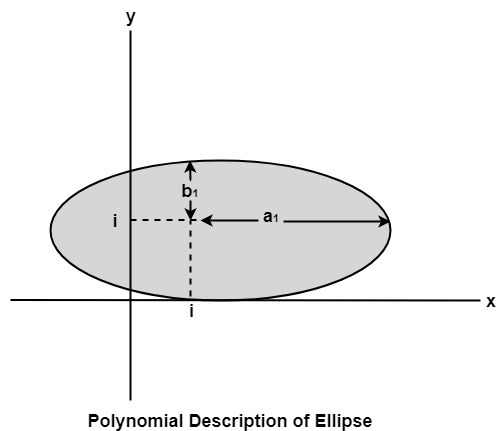
Polynomial Method
The ellipse has a major and minor axis. If a1 and b1are major and minor axis respectively. The centre of ellipse is (i, j). The value of x will be incremented from i to a1and value of y will be calculated using the following formula
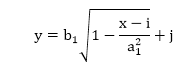
Drawback of Polynomial Method:
- It requires squaring of values. So floating point calculation is required.
- Routines developed for such calculations are very complex and slow.
Algorithm:
1. Set the initial variables: a = length of major axis; b = length of minor axis; (h, k) = coordinates of ellipse center; x = 0; i = step; xend = a.
2. Test to determine whether the entire ellipse has been scan-converted. If x>xend, stop.
Exception Handling in Java - Javatpoint
3. Compute the value of the y coordinate:
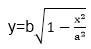
4. Plot the four points, found by symmetry, at the current (x, y) coordinates:
Plot (x + h, y + k) Plot (-x + h, -y + k) Plot (-y - h, x + k) Plot (y + h, -x + k)
5. Increment x; x = x + i.
6. Go to step 2.
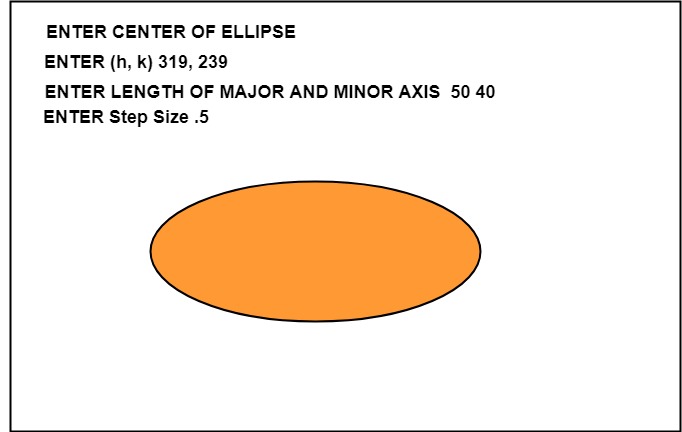
Program to draw an Ellipse using Polynomial Method:
- #include <graphics.h>
- #include <stdlib.h>
- #include <math.h>
- #include <stdio.h>
- #include <conio.h>
- #include <iostream.h>
- class bresen
- {
- float x, y, a, b, r, t, te, xend, h, k, step;
- public:
- void get ();
- void cal ();
- };
- void main ()
- {
- bresen b;
- b.get ();
- b.cal ();
- getch ();
- }
- void bresen :: get ()
- {
- cout<<"\n ENTER CENTER OF ELLIPSE";
- cout<<"\n enter (h, k) ";
- cin>>h>>k;
- cout<<"\n ENTER LENGTH OF MAJOR AND MINOR AXIS";
- cin>>a>>b;
- cout<<"\n ENTER Step Size";
- cin>> step;
- }
- void bresen ::cal ()
- {
- /* request auto detection */
- int gdriver = DETECT,gmode, errorcode;
- int midx, midy, i;
- /* initialize graphics and local variables */
- initgraph (&gdriver, &gmode, " ");
- /* read result of initialization */
- errorcode = graphresult ();
- if (errorcode ! = grOK) /*an error occurred */
- {
- printf("Graphics error: %s \n", grapherrormsg (errorcode);
- printf ("Press any key to halt:");
- getch ();
- exit (1); /* terminate with an error code */
- }
- x = 0;
- xend=a;
- whilex (x<xend)
- {
- t= (1-((x * x)/ (a * a)));
- if (t<0)
- te=-t;
- else
- te=t;
- y=b * sqrt (te);
- putpixel (h+x, k+y, RED);
- putpixel (h-x, k+y, RED);
- putpixel (h+x, y-y, RED);
- putpixel (h-x, k-y, RED);
- x+=step;
- }
- getch();
- }
Output: