Program to implement 2-D Transformations:

1. #include<iostream.h>  
2. #include<conio.h>  
3. #include<math.h>  
4. #include<stdlib.h>  
5. #include<conio.h>  
6. class trans  
7. {  
8.     float x[20],y[20],xm,ym,ref[2][2],shx,shy;  
9.     int i,j,k,n;  
10.     float sx,sy,tx,ty,ang;  
11.     int gd,gm;  
12.     float xtmp [20],ytmp[20];  
13.     public:  
14.     void takeinput();  
15.     void menu();  
16.     void graphmode();  
17.     void mapgraph();  
18.     void plotint();  
19.     void translate();  
20.     void scale();  
21.     void rotate();  
22.     void reflect();  
23.     void shear();  
24.     void plotfinal();  
25. };  
26. int ch;  
27. void trans::takeinput()  
28. {  
29.     cout<<"ENTER THE NO OF VERTICES\n";  
30.     cin>>n;  
31.     for (i=0;i<n;i++)  
32.     {  
33.         cout<<"ENTER THE "<<i+1<<"COORDINATES \n";  
34.         cin>>x[i]>>y[i];  
35.     }  
36.     clrscr();  
37. }  
38. void trans::menu()  
39. {  
40.     int kk;  
41.     cout<<"\n1:TRANSLATION";  
42.     cout<<"\n2:SCALING";  
43.     cout<<"\n3:ROTATION";  
44.     cout<<"\n4:REFLECTION";  
45.     cout<<"\n5:SHEARING";  
46.     cout<<"\n6:EXIT";  
47.     cin>>ch;  
48.     switch (ch)  
49.     {  
50.         case1:  
51.             cout<<"\n ENTER TX AND TY";  
52.             cin>>tx>>ty;  
53.             break;  
54.         case2:  
55.             cout<<"\n ENTER SX AND SY";  
56.             cin>>sx>>sy;  
57.             break;  
58.         case3:  
59.             cout<<"\n ENTER ANGLE OF ROTATION";  
60.             cin>>ang;  
61.             break;  
62.         case4:  
63.             cout<<"\n REFLECTION MENU";  
64.             cout<<"\n 1:X-PLANE";  
65.             cout<<"\n 2: Y-PLANE";  
66.             cout<<"\n 3: ORIGIN";  
67.             cout<<"\n 4: Y=X PLANE";  
68.             cout<<"\n 5: Y=-X PLANE";  
69.             cout<<"\n ENTER YOUR CHOICE";  
70.             cin>>kk;  
71.             switch (kk)  
72.             {  
73.                 case1:  
74.                          ref [0][0] =1;  
75.                     ref [0][1]=0;  
76.                     ref [1][0]=0;  
77.                     ref [1][1]=1;  
78.                     break;  
79.                 case2:  
80.                     ref [0][0]= -1;  
81.                     ref [0][1]=0;  
82.                     ref [1][0]=0;  
83.                     ref [1][1]=1;  
84.                     break;  
85.                 case3:  
86.                     ref [0][0]=-1;  
87.                     ref [0][1]=0;  
88.                     ref [1][0]=0;  
89.                     ref [1][1]=1;  
90.                     break;  
91.                 case4:  
92.                     ref [0][0]=0;  
93.                     ref [0][1]=1;  
94.                     ref [1][0] =1;  
95.                     ref [1][1]=0;  
96.                     break;  
97.                 case5:  
98.                     ref [0][0]=0;  
99.                     ref [0][1]=1;  
100.                     ref [1][0]=1;  
101.                     ref [1][1]=0;  
102.                     break;  
103.         case5:  
104.             cout<< "\n SHEARING MENU";  
105.             cout<<"\n 1:X-DIR\n 2: Y-DIR \n 3: X-Y DIR\n ENTER YOUR               CHOICE";  
106.             cin>>kk;  
107.             switch (kk)  
108.             {  
109.                 case1:  
110.                     cout<<"\n ENTER SHX";  
111.                     cin>> shx;  
112.                     ref[0][0] =1;  
113.                     ref [0][1]=0;  
114.                     ref [1][0]=shx;  
115.                     ref [1][1]=1;  
116.                     break;  
117.                 case2:  
118.                     cout<< "\n ENTER SHY";  
119.                     cin>>shy;  
120.                     ref [0][0]=1;  
121.                     ref [0][1]=shy;  
122.                     ref [1][0]=0;  
123.                     ref [1][1] =1;  
124.                     break;  
125.                 case3:  
126.                     cout<<"\n ENTER SHX";  
127.                     cin >> shx;  
128.                     cout<<"\n ENTER SHY";  
129.                     cin>> shy;  
130.                     ref [0][0] =1;  
131.                     ref [0][1] =shy;  
132.                     ref [1][0] =shx;  
133.                     ref [1][1] =1;  
134.                     break;  
135.                 }  
136.                 break;  
137.             }  
138.         }  
139.     void trans::graphmode()  
140.     {  
141.         gd=DETECT;  
142.         initgraph (&gd, &gm, "");  
143.     }  
144.     void trans::mapgraph()  
145.     {  
146.         xm=getmaxx ()/2;  
147.         ym=getmaxy ()/2;  
148.         line (xm,0,xm,2*ym);  
149.         line (0,ym,2 * xm,ym);  
150.     }  
151.     void trans::plotint()  
152.     {  
153.         for(i=0;i<n-1;i++)  
154.         {  
155.             circle (x[i] +xm,-y[i]+ym,2)  
156.             circle x [n-1]+xm,(-y[n-1]+ym),2;  
157.             line (x[i]+xm,(-y[i]+ym),x[i+1]+xm,(-y[i+1]+ym));  
158.         }  
159.         line (x[n-1]+xm,(-y[n-1]+ym,)x[0]+xm,(-y[0]+ym));  
160.     }  
161.     void trans::translate()  
162.     {  
163.         for(i=0;i<n;i++)  
164.         {  
165.             xtmp[i]=x[i]+tx;  
166.             ytmp[i]=y[i]+ty;  
167.         }  
168.     }  
169.     void trans::plotfinal()  
170.     {  
171.         for (i=0;i<n-1;i++)  
172.         {  
173.             circle (xtmp[i]+xm, (-ytmp[i]+ym,2);  
174.             circle (xtmp[n-1]+xm,(-ytmp[n-1]+ym),2);  
175.             line (xtmp[i]+xm,(-ytmp[i]+ym),xtmp[i+1]+xm,(-ytmp[i+1]+ym));  
176.         }  
177.             line (xtmp[n-1]+xm,(-ytmp[n-1]+ym),xtmp[0]+xm,(-ytmp[0]+ym));  
178.     }  
179.     void trans::scale()  
180.     {  
181.         float s [2][2],mxy[7][2],rxy[7][2];  
182.         s [0][0]=sx;  
183.         s [0][1]=0;  
184.         s [1][0]=0;  
185.         s [1][1]=sy;  
186.         tx=-x[0];  
187.         ty=-y[0];  
188.         translate ();  
189.         k=0;  
190.         for(i=0;i<n;i++)  
191.         {  
192.             j=0;  
193.             mxy[i][j]=xtmp[k];  
194.             mxy[i][j+1]=ytmp[k];  
195.             k++;  
196.         }  
197.         for (i=0;i<n;i++)  
198.         {  
199.             for(j=0;j<2;j++)  
200.             {  
201.                 rxy[i][j]=0;  
202.                 for(k=0;k<2;k++)  
203.                 {  
204.                     rxy[i][j]+=mxy[i][k]*s[k][j];  
205.                 }  
206.             }  
207.         }  
208.                 j=0;  
209.                 k=0;  
210.         for(i=0;i<n;i++)  
211.         {  
212.             j=0;  
213.             x[k]=rxy[i][j];  
214.             y[k]=rxy[i][j+1];  
215.             k++;  
216.         }  
217.         tx=-tx;  
218.         ty=-ty;  
219.         translate();  
220.     }  
221.     void trans::rotate()  
222.     {  
223.         float r[2][2],mxy[7][2],rxy[7][2],tmp;  
224.         tmp=22/7;  
225.         tmp=(tmp*ang)/180;  
226.         r[0][0]=cos(tmp);  
227.         r[0][1]=sin(tmp);  
228.         r[1][0]=cos(tmp);  
229.         r[1][1]=sy;  
230.         tx=-x[0];  
231.         ty=-y[0];  
232.         translate ();  
233.         k=0;  
234.         for (i=0;i<n;i++)  
235.           {  
236.         j=0;  
237.         mxy[i][j]=xtmp[k];  
238.         mxy[i][j+1]=ytmp[k];  
239.         k++;  
240.           }  
241.     for (i=0;i<n;i++)  
242.     {  
243.         for (j=0;j<2;j++)  
244.         {  
245.             rxy[i][j]=0;  
246.             for (k=0;k<2;k++)  
247.             {  
248.                 rxy[i][j]+=mxy[i][k]*r[k][j];  
249.             }  
250.         }  
251.     }  
252.         j=0;  
253.         k=0;  
254.     for(i=0;i<n;i++)  
255.     {  
256.         j=0;  
257.         x[k]=rxy[i][j];  
258.         y[k]=rxy[i][j+1];  
259.         k++;  
260.     }  
261.     tx=-tx;  
262.     ty=-ty;  
263.     translate();  
264. }  
265. void trans::reflect()  
266. {  
267.     float mxy[7][2],rxy[7][2],tmp;  
268.     tx=0;  
269.     ty=0;  
270.     translate();  
271.     k=0;  
272.     for(i=0;i<n;i++)  
273.     {  
274.         j=0;  
275.         mxy[i][j]=xtmp[k];  
276.         mxy[i][j+1]=ytmp[k];  
277.         k++;  
278.     }  
279.     for(i=0;i<n;i++)  
280.     {  
281.         for(j=0;j<2;j++)  
282.         {  
283.             rxy[i][j]=0;  
284.             for(k=0;k<2;k++)  
285.             {  
286.                 rxy[i][j]|+=mxy[i][k]*r[k][j];  
287.             }  
288.         }  
289.     }  
290.         j=0;  
291.         k=0;  
292.     for(i=0;i<n;i++)  
293.     {  
294.         j=0;  
295.         x[k]=rxy[i][j];  
296.         y[k]=rxy[i][j+1];  
297.         k++;  
298.     }  
299.     tx=-tx;  
300.     ty=-ty;  
301.     translate();  
302. }  
303. void trans::shear()  
304. {  
305.     float mxy[7][2],rxy[7][2],tmp;  
306.     tx=0;  
307.     ty=0;  
308.     translate ();  
309.     k=0;  
310.     for(i=0;i<n;i++)  
311.     {  
312.         j=0;  
313.         mxy[i][j]=xtmp[k];  
314.         mxy[i][j+1]=ytmp[k];  
315.         k++;  
316.     }  
317.     for(i=0;i<n;i++)  
318.     {  
319.         for(j=0;j<2;j++)  
320.         {  
321.             rxy[i][j]=0;  
322.             for (k=0;k<2;k++)  
323.             {  
324.                 rxy[i][j]|+=mxy[i][k]*r[k][j];  
325.             }  
326.         }  
327.     }  
328.         j=0;  
329.         k=0;  
330.     for(i=0;i<n;i++)  
331.     {  
332.         j=0;  
333.         x[k]=rxy[i][j];  
334.         y[k]=rxy[i][j+1];  
335.         k++;  
336.     }  
337.     tx=-tx;  
338.     ty=-ty;  
339.     translate ();  
340. }  
341. void main()  
342. {  
343.     clrscr ();  
344.     trans t1;  
345.     t1.takeinput ();  
346.     t1.menu ();  
347.     t1.graphmode ();  
348.     t1.mapgraph ();  
349.     t1.plotint ();  
350.     switch (ch)  
351.     {  
352.         case1:  
353.             t1.translate ();  
354.             break;  
355.         case2:  
356.             t1.scale ();  
357.             break ();  
358.         case3:  
359.             t1.rotate ();  
360.             break;  
361.         case4:  
362.             t1.reflect ();  
363.             break;  
364.         case5:  
365.             t1.shear ();  
366.             break;  
367.         case6:  
368.             exit ();  
369.         }  
370.         getch ();  
371.         t1.plotfinal ();  
372.         getch ();  
373.         closegraph ();  
374. }  

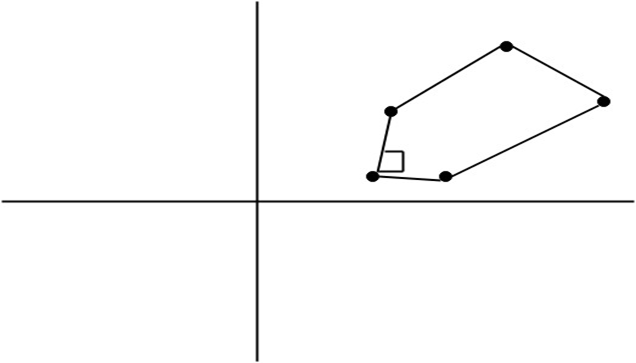
Output:

Translate

1: TRANSLATION
2: SCALING
3: ROTATION
4: REFLECTION
5: SHEARING
6: EXIT
ENTER YOUR CHOICE 4
REFLECTION MENU
1: X-PLANE
2: Y-PLANE
3: ORIGIN
4: Y=X PLANE
5: Y=-X PLANE
ENTER YOUR CHOICE 4
1: TRANSLATION
2: SCALING
3: ROTATION
4: REFLECTION
5: SHEARING
6: EXIT
ENTER YOUR CHOICE 5
SHEARING MENU
1: X-DIR
2: Y-DIR
ENTER YOUR CHOICE 3

ENTER SHX 5
ENTER SHY 5
ENTER THE NO OF VERTICES
5
ENTER THE 1 COORDINATES
10 10
ENTER THE 2 COORDINATES
30 10
ENTER THE 3 COORDINATES
40 20
ENTER THE 4 COORDINATES
35 30
ENTER THE 5 COORDINATES
15 20
1: TRANSLATION
2: SCALING
3: ROTATION
4: REFLECTION
5: SHEARING
6: EXIT
ENTER YOUR CHOICE 1
ENTER TX AND TY 10 10

Polymorphism in Java | Dynamic Method Dispatch