Shading is referred to as the implementation of the illumination model at the pixel points or polygon surfaces of the graphics objects.

Shading model is used to compute the intensities and colors to display the surface. The shading model has two primary ingredients: properties of the surface and properties of the illumination falling on it. The principal surface property is its reflectance, which determines how much of the incident light is reflected. If a surface has different reflectance for the light of different wavelengths, it will appear to be colored.

An object illumination is also significant in computing intensity. The scene may have to save illumination that is uniform from all direction, called diffuse illumination.

Difference between JDK, JRE, and JVM

Shading models determine the shade of a point on the surface of an object in terms of a number of attributes. The shading Mode can be decomposed into three parts, a contribution from diffuse illumination, the contribution for one or more specific light sources and a transparency effect. Each of these effects contributes to shading term E which is summed to find the total energy coming from a point on an object. This is the energy a display should generate to present a realistic image of the object. The energy comes not from a point on the surface but a small area around the point.

The simplest form of shading considers only diffuse illumination:

              E_pd=R_p I_d

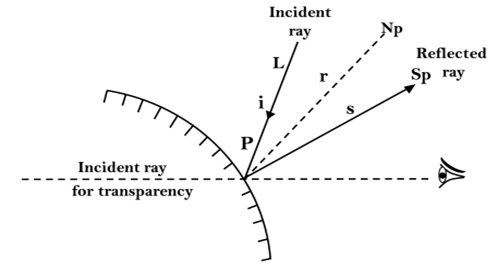
where E_pd is the energy coming from point P due to diffuse illumination. I_d is the diffuse illumination falling on the entire scene, and R_p is the reflectance coefficient at P which ranges from shading contribution from specific light sources will cause the shade of a surface to vary as to its orientation concerning the light sources changes and will also include specular reflection effects. In the above figure, a point P on a surface, with light arriving at an angle of incidence i, the angle between the surface normal N_p and a ray to the light source. If the energy I_ps arriving from the light source is reflected uniformly in all directions, called diffuse reflection, we have

              E_ps=(R_p cos i)I_ps

This equation shows the reduction in the intensity of a surface as it's tipped obliquely to the light source. If the angle of incidence i exceeds90°, the surface is hidden from the light source and we must set E_psto zero.