It came under the category of list priority algorithm. It is also called a depth-sort algorithm. In this algorithm ordering of visibility of an object is done. If objects are reversed in a particular order, then correct picture results.

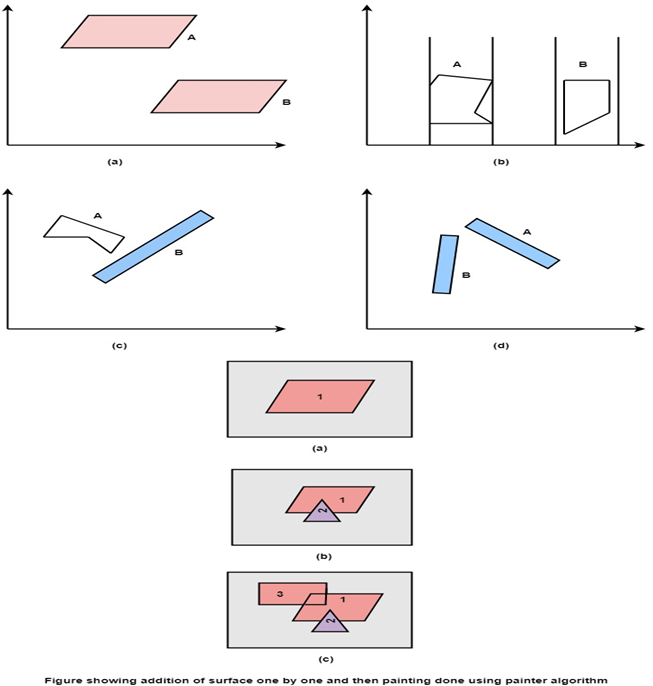
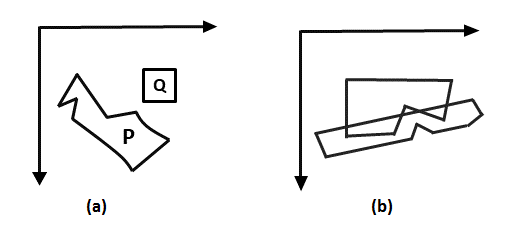
Objects are arranged in increasing order to z coordinate. Rendering is done in order of z coordinate. Further objects will obscure near one. Pixels of rear one will overwrite pixels of farther objects. If z values of two overlap, we can determine the correct order from Z value as shown in fig (a).

If z objects overlap each other as in fig (b) this correct order can be maintained by splitting of objects.

Depth sort algorithm or painter algorithm was developed by Newell, sancha. It is called the painter algorithm because the painting of frame buffer is done in decreasing order of distance. The distance is from view plane. The polygons at more distance are painted firstly.

The concept has taken color from a painter or artist. When the painter makes a painting, first of all, he will paint the entire canvas with the background color. Then more distance objects like mountains, trees are added. Then rear or foreground objects are added to picture. Similar approach we will use. We will sort surfaces according to z values. The z values are stored in the refresh buffer.

Steps performed in-depth sort

1. Sort all polygons according to z coordinate.
2. Find ambiguities of any, find whether z coordinate overlap, split polygon if necessary.
3. Scan convert each polygon in increasing order of z coordinate.

Painter Algorithm

Step1: Start Algorithm

Step2: Sort all polygons by z value keep the largest value of z first.

Step3: Scan converts polygons in this order.
                Test is applied

1. Does A is behind and non-overlapping B in the dimension of Z as shown in fig (a)
2. Does A is behind B in z and no overlapping in x or y as shown in fig (b)
3. If A is behind B in Z and totally outside B with respect to view plane as shown in fig (c)
4. If A is behind B in Z and B is totally inside A with respect to view plane as shown in fig (d)

The success of any test with single overlapping polygon allows F to be painted.